Makine Öğrenmesi Bölüm 2

Makine Öğrenmesinde Regresyon ve Sınıflandırma

Makine öğrenmesinde regresyon ve sınıflandırma, farklı türdeki problemlere çözüm sunan iki temel model türüdür.

Regresyon:

Regresyon, sürekli sayısal verileri tahmin etmek için kullanılan bir makine öğrenmesi tekniğidir. Bu yöntemde amaç, bağımsız değişkenler arasındaki ilişkiyi analiz ederek bağımlı değişkenin değerini tahmin etmektir. Örneğin, ev fiyatlarını tahmin etmek, bir şirketin gelecekteki gelirlerini öngörmek veya hava sıcaklıklarını tahmin etmek regresyon problemlerine örnek olarak verilebilir. En yaygın regresyon tekniklerinden bazıları doğrusal regresyon, lojistik regresyon ve çoklu regresyondur.

Sınıflandırma:

Sınıflandırma, verilerin belirli kategorilere veya sınıflara ayrılması için kullanılan bir makine öğrenmesi yöntemidir. Burada amaç, verilen veriyi analiz ederek doğru sınıfa atamaktır. Sınıflandırma problemlerine örnek olarak e-postaların spam olup olmadığını belirlemek, müşteri davranışlarına göre satın alma olasılığını tahmin etmek veya görsel tanıma sistemlerinde nesneleri tanımlamak verilebilir. Sınıflandırmada kullanılan yaygın algoritmalar arasında Karar Ağaçları, Destek Vektör Makineleri (SVM) ve Naive Bayes (Bayes teoremine dayanan, özelliklerin birbirinden bağımsız olduğunu varsayarak sınıflandırma yapan olasılıksal bir algoritma) bulunur.

Makine Öğrenmesi Model İşlevleri

fit()

fit() yöntemi, makine öğrenmesi modellerinin eğitilmesi için kullanılır. Model, eğitim verilerini ve hedef değerleri kullanarak kendini bu verilere göre ayarlar ve öğrenir. Örneğin, bir regresyon veya sınıflandırma modelinde, fit() çağrıldığında model, eğitim verileriyle öğrendiği kuralları oluşturur.

Örnek Kod: Doğrusal Regresyon Modeli Eğitimi

Gerekli kütüphanelerin import edilmesi

from sklearn.model_selection import train_test_split
from sklearn.datasets import make_regression
import matplotlib.pyplot as plt

Rastgele bir veri seti oluşturulması

X, y = make_regression(n_samples=100, n_features=1, noise=10, random_state=42)

Veriyi eğitim ve test setlerine ayırma

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

Doğrusal Regresyon modelini oluşturma

model = LinearRegression()

Modeli eğitim verileri ile eğitme (fit etme)

model.fit(X_train, y_train)

Test verileri üzerinde tahmin yapma

predictions = model.predict(X_test)

Modelin performansını görselleştirme

plt.scatter(X_test, y_test, color='blue', label='Gerçek Değerler')
plt.plot(X_test, predictions, color='red', label='Tahmin Edilen Değerler')
plt.xlabel('Özellik')
plt.ylabel('Hedef')
plt.title('Doğrusal Regresyon Modeli')
plt.legend()
plt.show()

Kod Açıklaması:

1. Veri Oluşturma: make_regression fonksiyonu ile rastgele bir veri seti oluşturuluyor.
2. Veri Bölme: train_test_split ile veri, eğitim ve test setlerine ayrılıyor.
3. Model Oluşturma: LinearRegression sınıfından bir model oluşturuluyor.
4. Modeli Eğitme: ; fit() yöntemi, eğitim verileriyle (X_train ve y_train) modeli eğitiyor.
5. Tahmin: Eğitilen model, test verileri üzerinde tahmin yapıyor.
6. Görselleştirme: Gerçek değerler ve tahmin edilen değerler görselleştiriliyor.

score()

score() yöntemi, modelin performansını değerlendirmek için kullanılır. Bu yöntem, modelin eğitim veya test verileri üzerinde ne kadar iyi performans gösterdiğini ölçer. Örneğin, sınıflandırma problemlerinde doğruluk oranı, regresyon problemlerinde ise R-kare değeri gibi ölçümlerle sonuç verir.

Örnek Kod: Doğrusal Regresyon Modeli Performans Değerlendirmesi

Gerekli kütüphanelerin import edilmesi

from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_regression
import numpy as np

Rastgele bir veri seti oluşturulması

X, y = make_regression(n_samples=100, n_features=1, noise=10, random_state=42)

Veriyi eğitim ve test setlerine ayırma

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

Doğrusal Regresyon modelini oluşturma

model = LinearRegression()

Modeli eğitim verileri ile eğitme (fit etme)

model.fit(X_train, y_train)

Eğitim seti üzerindeki performansı değerlendirme

train_score = model.score(X_train, y_train)

Test seti üzerindeki performansı değerlendirme

test_score = model.score(X_test, y_test)

Performans sonuçlarını yazdırma

print(f"Modelin Eğitim Seti R-kare Değeri: {train_score:.2f}")
print(f"Modelin Test Seti R-kare Değeri: {test_score:.2f}")

Kod Açıklaması:

1. Veri Oluşturma: make_regression ile rastgele bir veri seti oluşturuluyor.
2. Veri Bölme: train_test_split ile veri, eğitim ve test setlerine ayrılıyor.
3. Model Oluşturma ve Eğitme: LinearRegression sınıfından oluşturulan model, fit() yöntemi ile eğitiliyor.
4. Performans Değerlendirme: score() yöntemi, hem eğitim hem de test setleri üzerinde modelin R-kare (R²) değerini hesaplıyor. R-kare değeri, modelin veri üzerindeki tahmin doğruluğunu gösterir. 1’e ne kadar yakınsa, modelin o kadar iyi olduğunu belirtir.

predict()

predict() yöntemi, eğitilmiş bir modelin, yeni veya görülmemiş veriler üzerinde tahmin yapmasını sağlar. Model, `fit() ile öğrendiği kurallara dayanarak verilen girdilere karşılık gelen çıktıları tahmin eder. Örneğin, bir sınıflandırma modelinde hangi sınıfa ait olduğunu, bir regresyon modelinde ise beklenen sayısal değeri tahmin eder.

Örnek Kod: Doğrusal Regresyon Modeli ile Tahmin Yapma

Gerekli kütüphanelerin import edilmesi

from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_regression
import matplotlib.pyplot as plt

Rastgele bir veri seti oluşturulması

X, y = make_regression(n_samples=100, n_features=1, noise=10, random_state=42)

Veriyi eğitim ve test setlerine ayırma

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

Doğrusal Regresyon modelini oluşturma

model = LinearRegression()

Modeli eğitim verileri ile eğitme (fit etme)

model.fit(X_train, y_train)

Test seti üzerindeki tahminleri yapma

predictions = model.predict(X_test)

Tahmin sonuçlarını görselleştirme

plt.scatter(X_test, y_test, color='blue', label='Gerçek Değerler')
plt.scatter(X_test, predictions, color='red', label='Tahminler', marker='x')
plt.xlabel('Özellik')
plt.ylabel('Hedef')
plt.title('Doğrusal Regresyon Modeli Tahminleri')
plt.legend()
plt.show()

Tahmin değerlerini yazdırma

print("Gerçek Değerler:", y_test[:5])
print("Tahmin Değerleri:", predictions[:5])

Kod Açıklaması:

1. Veri Oluşturma: make_regression ile rastgele bir veri seti oluşturuluyor.
2. Veri Bölme: train_test_split ile veri, eğitim ve test setlerine ayrılıyor.
3. Model Oluşturma ve Eğitme: LinearRegression sınıfından oluşturulan model, fit() yöntemi ile eğitiliyor.
4. Tahmin Yapma: predict() yöntemi, test setindeki verilere karşılık gelen tahminleri yapıyor.
5. Görselleştirme: Gerçek ve tahmin edilen değerler görsel olarak karşılaştırılıyor.
6. Sonuçları Yazdırma: İlk beş gerçek ve tahmin değerleri yazdırılarak sonuçların incelenmesi sağlanıyor.

Underfitting, Overfitting ve Balanced Fitting Nedir?

Makine öğrenmesi modelleri geliştirilirken doğru dengeyi sağlamak çok önemlidir. Bu bağlamda, underfitting, overfitting ve balanced fitting terimleri, bir modelin veriyi nasıl öğrendiğini ve bu öğrenmenin modelin performansını nasıl etkilediğini ifade eder:

Underfitting (Yetersiz Öğrenme):

Underfitting, modelin eğitim verilerini yeterince iyi öğrenememesi ve dolayısıyla düşük performans göstermesi durumudur. Model, veriler arasındaki ilişkileri ve desenleri yakalayamadığı için hem eğitim hem de test verisi üzerinde kötü sonuçlar verir. Genellikle modelin karmaşıklığının yetersiz olduğu, çok az veriyle veya çok basit bir modelle çalışıldığı durumlarda ortaya çıkar. Bu tür modeller genellikle doğru tahmin yapamaz.

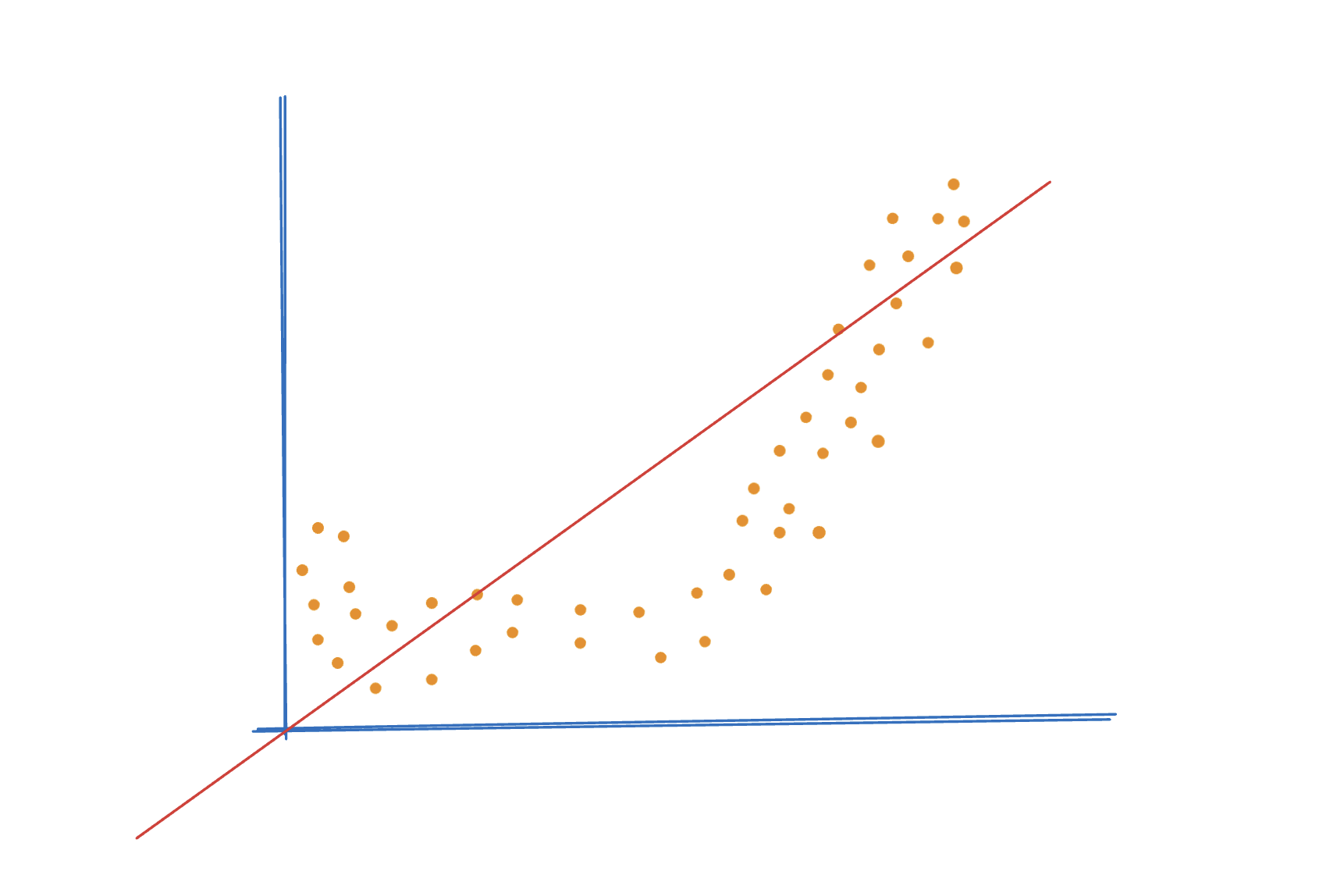
Overfitting (Aşırı Öğrenme):

Overfitting, modelin eğitim verilerini aşırı derecede öğrenmesi, hatta ezberlemesi durumudur. Model, eğitim verisindeki gürültü ve rastgelelikleri de öğrenerek, bu verilere çok iyi uyum sağlar; ancak, yeni ve görülmemiş veriler üzerinde genellikle kötü performans gösterir. Overfitting, modelin karmaşıklığının gereğinden fazla olduğu, çok fazla parametreye sahip modellerin kullanıldığı veya çok az veriyle eğitildiği durumlarda meydana gelir.

Balanced Fitting (Dengeli Öğrenme):

Balanced fitting, modelin hem eğitim hem de test verileri üzerinde iyi performans gösterdiği, veriyi aşırı öğrenmeden veya yetersiz öğrenmeden optimum şekilde öğrendiği durumu ifade eder. Dengeli bir model, verinin genel desenlerini doğru bir şekilde yakalar ve genelleme yapma yeteneğine sahiptir. Bu, iyi bir model seçimi, doğru miktarda eğitim verisi kullanımı ve uygun hiperparametre ayarlamaları ile sağlanır.

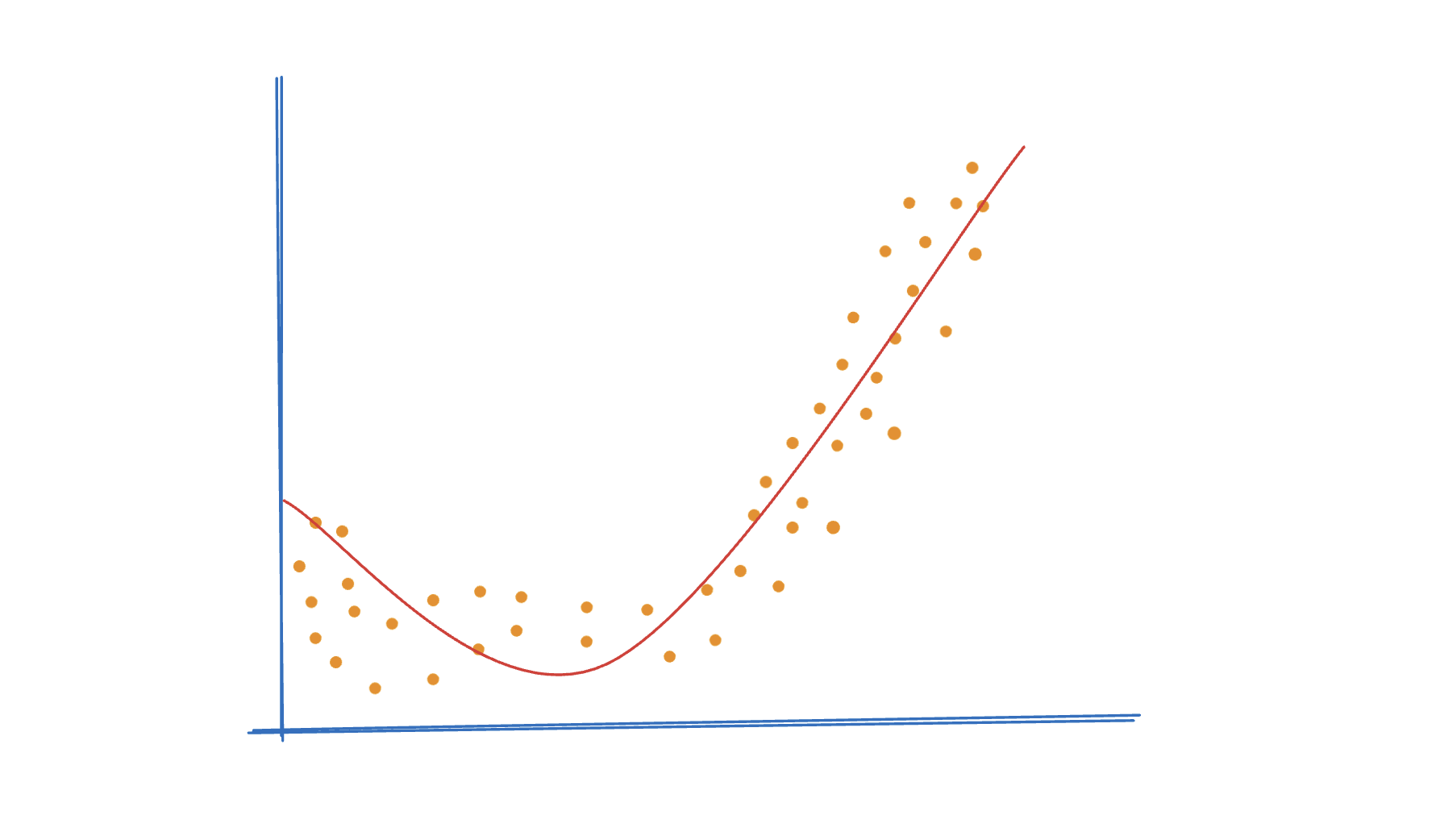
Bu kavramlar, modelin başarısını artırmak ve doğru tahminler yapmak için modelin karmaşıklığını ve eğitim sürecini optimize etmenin önemini vurgular.